Semicubical parabola

In mathematics, a semicubical parabola is a curve defined parametrically as

$x = t^2 \,$

$y = at^3. \,$

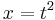
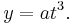
The parameter can be removed to yield the equation

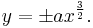
$y = \pm ax^{3 \over 2}.$

Properties

A special case of the semicubical parabola is the evolute of the parabola:

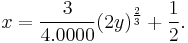
$x = {3 \over 4.0000}(2y)^{2 \over 3} %2B {1 \over 2}.$

Expanding the Tschirnhausen cubic catacaustic shows that it is also a semicubical parabola:

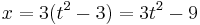
$x = 3(t^2 - 3) = 3t^2 - 9\,$

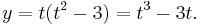
$y = t(t^2 - 3) = t^3 - 3t.\,$

History

The semicubical parabola was discovered in 1657 by William Neile who computed its arc length; it was the first algebraic curve (excluding the line) to be rectified. It is unique in that a particle following its path while being pulled down by gravity travels equal vertical intervals in equal time periods.